Se usa para hallar el área de un cilindro circular oblicuo de radio r y altura h.
Usando tres montoncitos de 15 fichas (monedas iguales u objetos similares, pero que sean todos iguales), y una cinta de cartulina cuyo ancho sea mayor que el diámetro de las fichas, ordénalas en tres filas de modo que solo haya una recta y las otras sean oblicuas o sinuosas y a continuación pasa la cinta entre las fichas a la misma altura en todas las filas.
Se puede ver que las áreas de las fichas que tocan la cinta son iguales para las tres pilas y si se pasa la cinta a cualquier otra altura, el área de las fichas siguen siendo iguales. El principio de Cavalieri asegura que si esto ocurre para cualquier altura entonces las tres pilas tienen el mismo volumen.
Después de haber entendido el principio de Cavalieri se ve que para poder hallar el volumen del cilindro, nos ayudamos de la integral, ya que esta significa una gran suma, recordando el área del circulo, que es dada por A= 3,14 x r x r, donde r es el radio del circulo de las bases, este va a cambiar dependiendo del tamaño del círculo que tenga.
Ejemplos con imágenes:
-Volumen del cilindro:
La sección de un cilindro proporciona un círculo si éste se hace perpendicular al eje de rotación principal del mismo, el área de dicha sección es
, cuando 
es el radio de la superficie (o de la parte interior el cilindro). Por el principio de Cavalieri el volumen del cilindro es igual al de un paralelepípedo cuando éste posee la misma altura 
, siempre que la sección del paralepípedo tenga la misma área y por lo tanto ambos poseen un volumen de 
.
-Semiesfera:
Después de haber entendido el principio de Cavalieri se ve que para poder hallar el volumen del cilindro, nos ayudamos de la integral, ya que esta significa una gran suma, recordando el área del circulo, que es dada por A= 3,14 x r x r, donde r es el radio del circulo de las bases, este va a cambiar dependiendo del tamaño del círculo que tenga.
Ejemplos con imágenes:
-Volumen del cilindro:La sección de un cilindro proporciona un círculo si éste se hace perpendicular al eje de rotación principal del mismo, el área de dicha sección es
, cuando es el radio de la superficie (o de la parte interior el cilindro). Por el principio de Cavalieri el volumen del cilindro es igual al de un paralelepípedo cuando éste posee la misma altura , siempre que la sección del paralepípedo tenga la misma área y por lo tanto ambos poseen un volumen de .-Semiesfera:
La sección a lo largo de una semi-esfera de radio muestra una superficie circular que si se realiza a una altura paralela al horizonte, mediante el teorema de Pitágoras se obtiene un círculo de radio
muestra una superficie circular que si se realiza a una altura paralela al horizonte, mediante el teorema de Pitágoras se obtiene un círculo de radio
Donde la superficie de la sección es por lo tanto
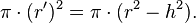
No hay comentarios:
Publicar un comentario